注釈

このページは docs/tutorials/02_portfolio_diversification.ipynb から生成されました。

ポートフォリオの分散#

はじめに#

資産運用には、大きく分けてアクティブ運用とパッシブ運用の２つのアプローチがあります。 パッシブ運用には、インデックスに連動するファンドや、多数の資産をより少ない代表銘柄で表現するポートフォリオ分散に基づくアプローチがあります。 このノートブックでは、2つの理由から最近人気が出てきているポートフォリオの分散問題を解説しています。 1. 限られた取引コストと限られた予算で、インデックス（または同様に大規模な資産の集合）のパフォーマンスを模倣することが可能になります。 つまり、従来のインデックス・トラッキングでは、インデックス内のすべての資産を、理想的にはインデックスと同じ重みで購入することができます。 これは、いくつかの理由により実用的ではない場合があります。つまり、 1 つの資産につき 1 回のラウンドロットの合計でさえ、運用資産を超える場合がありこと、積分制約によるインデックス・トラッキングの問題が大きいため最適化の問題が困難になる可能性がありこと、インデックス内の重みに対する位置を調整するために頻繁にリバランスされる取引コストによって、この手法が高価になる可能性があります。 このため、 \(n\) の資産を代表する \(q\) の資産のポートフォリオを、 \(q\) が \(n\) よりも大幅に下回るよう選択することにより、ポートフォリオが基盤となる市場の動きを再現するというアプローチが定着しています。 資産を \(q\) クラスターにグループ化する方法と、 \(q\) 個の資産を判別する方法を決定するには、大規模な最適化問題を解決するために、\(q\) クラスターを表す必要があります。 以下では、ポートフォリオの投資分散に関する問題の数学的モデルについて説明します。[Cornuejols & Tutuncu, 2006] 2. これにより、共分散行列を超えた時系列間の類似度の測定が可能になります。 伝統的に、現代ポートフォリオ理論では、資産間の類似性の指標としての共分散行列が考慮されていることに注意してください。 しかし、そのような場合には、共分散行列は不完全です。 例えば、ロンドンとニューヨークの両方に上場している会社を考えてみましょう。両方の上場銘柄は非常に似ているはずですが、市場が開く時間が部分的に重なっているため、2つの上場銘柄の価格の時系列の一部だけが重なります。共分散の代わりに、2つの時系列間の類似性の尺度として、例えば[Berndt and Clifford, 1994]の動的時間伸縮法（DTW）を考慮することができます。これにより、ある期間において、データは時系列の 1 つのみによって捕捉され、その他の期間については、両方の時系列が株価の同時進行による類似性を示すと考えることができます。

全体的なワークフローは以下のとおりです。

  1. 資産の基本セットを選択します。ここでは、少数の米国株です。

  2. 資産の価格の変動を把握する時系列をロードします。 ここでは、Wikipedia 、Nasdaq、 LSE 、またはEuroNextから取得した調整された日々の終値データを単純化したもので、実際の資産管理においては、より高い頻度を考慮する必要があることにご注意ください。

  3. 時系列間のペアごとの類似性を計算します。 ここでは、まだ古典コンピュータ上での動的時間伸縮法（DTW）の線形近似を実行しています。

  4. 類似度の測定方法に基づいて、 \(q\) の代表資産の実際のポートフォリオを計算します。 このステップは2 回実行されます。 まず、 IBMの最適化ソルバー (IBM ILOG CPLEX または Exact Eigensolver) の古典コンピューターでの実行による参照値を取得します。 次に、量子コンピュータ上で部分的に代替のハイブリッドアルゴリズムを実行します。

  5. 結果を視覚化します。 ここでは単純なプロットをします。

以下では、前提条件とデータロードのインストールを進める前に、上記(4) で使用されているモデルについて、説明します。

モデル#

[Cornuejols & Tutuncu, 2006] で議論されているように、資産を類似した資産グループにクラスター化し、各グループから代表的な１資産を選択してインデックス・ファンドのポートフォリオに組み入れる数理モデルを記述します。このモデルは以下のデータに基づいており、後に詳述します。

\[\rho_{ij} = \textrm{similarity}\, \textrm{between}\, \textrm{stock}\, i \, \textrm{and}\, \textrm{stock}\, j.\]

例えば、 \(i \neq j\) とした場合、 \(\rho_{ii} = 1\), \(\rho_{ij} \leq 1\) であるならば、 \(\rho_{ij}\) は類似する銘柄ほど大きな値になります。 これは銘柄のリターン \(i\) と \(j\) の相関を表す場合に使うことができます。この時、別の類似性指数 \(\rho_{ij}\) を選ぶこともできます。

私たちが解決したい問題は次のとおりです。:

\[(M) \quad f = \max_{x_{ij}, y_{j}} \,\, \sum_{i=1}^n \sum_{j=1}^n \rho_{ij} x_{ij}\]

クラスタリング制約の条件:

\[\sum_{j=1}^n y_j = q,\]

整合性制約:

\[\sum_{j=1}^n x_{ij} = 1, \,\textrm{ for }\, i = 1,\ldots, n, \quad x_{ij} \leq y_j,\,\textrm{ for }\, i = 1,\ldots, n; \, j = 1,\ldots, n, \quad x_{jj} = y_j,\,\textrm{ for }\, j = 1,\ldots, n,\]

および積分制約:

\[\quad x_{ij}, y_j \in\{0,1\}, \,\textrm{ for }\, i = 1,\ldots, n; \, j = 1,\ldots, n.\]

変数 \(y_j\) は、どの銘柄 \(j\) がインデックスファンドの中にあるかを表します (ファンドの中で \(j\) が選択されている場合は \(y_j = 1\) 、そうでない場合は \(0\) )。各銘柄 \(i = 1,\dots,n\), について、変数 \(x_{ij}\) は、どの銘柄 \(j\) が \(i\) とよく似ているのかを表します(インデックスファンド内で \(j\) が最も似ている銘柄の場合は \(x_{ij} = 1\) 、そうでない場合は \(0\) )。

第一の制約は、ファンドの中で \(q\) 株を選択します。第二の制約は、各株式 \(i\) がファンド内に正確に 1 つの代表的な株式 \(j\) を持つことを課します。第三の制約と第四の制約は、株式 \(j\) がファンド内に存在する場合に限り、株式 \(j\) が \(i\) を代表することができることを保証します。モデルの目的は、ファンド内の \(n\) 株とその代表株との類似性を最大化することで、異なるコスト関数も考慮することができます。

決定変数を1つのベクトルに連結してみましょう。

\[{\bf z} = [x_{11},x_{12},\ldots,x_{1n}, x_{22},\ldots,x_{nn}, y_{1},\ldots,y_{n}],\]

次元が \(z\in\{0,1\}^N\), with \(N = n (n+1)\) とし、最適解を \(z^*\) 、 最適コスト \(f^*\) とする。

ハイブリッドアプローチ#

ここでは、Farhi、Goldstone、Gutmann (2014) の量子近似最適化アプローチに従って、古典的な計算ステップと量子計算のステップを組み合わせたアプローチを示します。

バイナリー多項式最適化の構築#

\((M)\) から、 \(x_{ij} \leq y_j\) 不等式制約を、等価な等式制約 \(x_{ij} (1- y_j) = 0\) に置き換えることで、等式制約のみを持つ二項式最適化を構築することができます。 すると、問題は次のようになります。

\[(BPO) \quad f = \max_{x_{ij}, y_{j}} \,\, \sum_{i=1}^n \sum_{j=1}^n \rho_{ij} x_{ij}\]

クラスタリング制約、積分制約、および次の修正された整合性制約に従います。

\[\sum_{j=1}^n x_{ij} = 1, \,\textrm{ for }\, i = 1,\ldots, n,\]
\[\quad x_{ij} (1- y_j) = 0,\,\textrm{ for }\, i = 1,\ldots, n; \, j = 1,\ldots, n,\]
\[\quad x_{jj} = y_j,\,\textrm{ for }\, j = 1,\ldots, n.\]

イジング・ハミルトニアンの構築#

これで、イジング・ハミルトニアン(QUBO)をペナルティメソッド(各等価性制約に対してペナルティ係数 \(A\) を導入)で次のように構成することができるようになりました。

\[(IH) \quad H = \sum_{i=1}^n \sum_{j=1}^n \rho_{ij} x_{ij} + A\Big( \sum_{j=1}^n y_j - q\Big)^2 + \sum_{i=1}^n A\Big( \sum_{j=1}^n x_{ij} - 1\Big)^2 + \sum_{j=1}^n A (x_{jj}-y_j)^2 +\sum_{i=1}^n \sum_{j=1}^n A \left(x_{ij} (1- y_j)\right).\]

ハミルトニアンから二次計画法（QP）定式化へ#

ベクトル \({\bf z}\) では、イジング・ハミルトニアンの要素を次のように書き換えることができます。

最初の項：

\[\sum_{i=1}^n \sum_{j=1}^n \rho_{ij} x_{ij} = [\rho_{11},\rho_{12},\ldots,\rho_{1n}, \rho_{22},\ldots,\rho_{nn}|{\bf 0}_n ]{\bf z} =: {\bf c}_0^T {\bf z}\]

第二の項：

\[\begin{split}A\Big( \sum_{j=1}^n y_j - q\Big)^2 = A \Big(\sum_{j=1}^n y_j\Big)^2 - 2 Aq \sum_{j=1}^n y_j + A q^2 = A {\bf z}^T \left[\begin{array}{c}{\bf 0}_{n^2} \\ \hline {\bf 1}_n \end{array}\right]\left[\begin{array}{cc}{\bf 0}_{n^2} | {\bf 1}_n \end{array}\right]{\bf z} - 2 A q [{\bf 0}_{n^2}|{\bf 1}_n]{\bf z} + A q^2 =: {\bf z}^T {\bf Q}_0 {\bf z} + {\bf c}_1^T {\bf z} + r_0\end{split}\]

第三の項：

\[\sum_{i=1}^n A\Big( \sum_{j=1}^n x_{ij} - 1\Big)^2 = A\sum_{i=1}^n \Big(\sum_{j=1}^n x_{ij}\Big)^2 - 2 A \sum_{i=1}^n\sum_{j=1}^n x_{ij} + n A = \qquad\qquad\qquad\qquad\qquad\qquad\qquad\]

これは、以下と同等です：

\[\begin{split}\qquad\qquad\qquad\qquad\qquad\qquad\qquad = A {\bf z}^T \left(\sum_{i=1}^n \left[\begin{array}{c}{\bf 0}_{n(i-1)} \\ {\bf 1}_n \\ {\bf 0}_{n(n-i)} \\ \hline {\bf 0}_{n} \end{array}\right]\left[\begin{array}{cccc}{\bf 0}_{n(i-1)} & {\bf 1}_n & {\bf 0}_{n(n-i)} & | {\bf 0}_{n} \end{array}\right]\right){\bf z} - 2 A [{\bf 1}_{n^2}|{\bf 0}_n]{\bf z} + n A =: {\bf z}^T {\bf Q}_1 {\bf z} + {\bf c}_2^T {\bf z} + r_1\end{split}\]

第四の項：

\[\begin{split}A \sum_{j=1}^n (x_{jj}-y_j)^2 = A {\bf z}^T \left(\sum_{j=0}^{n-1} \left[\begin{array}{c}{\bf 0}_{nj + j} \\ 1 \\ {\bf 0}_{n^2-(nj+j+1)} \\ \hline {\bf 0}_{j} \\ -1 \\ {\bf 0}_{n-j-1} \end{array}\right]\left[\begin{array}{cccccc}{\bf 0}_{nj + j} & 1 & {\bf 0}_{n^2-(nj+j+1)} & | {\bf 0}_{j} & -1 & {\bf 0}_{n-j-1} \end{array}\right]\right){\bf z} = A {\bf z}^T {\bf Q}_2 {\bf z}\end{split}\]

第五の項：

\[\begin{split}\sum_{i=1}^n \sum_{j=1}^n A \left(x_{ij} (1- y_j)\right) = A [{\bf 1}_{n^2}|{\bf 0}_n]{\bf z} + A {\bf z}^T \left( \sum_{i=1}^n \sum_{j=1}^n \left[\begin{array}{ccc|c} & & & \\ & {\bf 0}_{n^2\times n^2} & & -1/2_{(ij,j)} \\ & & & \\ \hline & -1/2_{(j, ij)} & & {\bf 0}_{n} \end{array}\right] \right) {\bf z} =: {\bf z}^T {\bf Q}_3 {\bf z} + {\bf c}_3^T {\bf z}\end{split}\]

これにより、定式化は以下のようになります。

\[(IH-QP)\quad \max_{{\bf z}\in\{0,1\}^{n(n+1)}} \, {\bf z}^T ({\bf Q}_0+{\bf Q}_1+ {\bf Q}_2 + {\bf Q}_3 ){\bf z} + ({\bf c}_0+{\bf c}_1+{\bf c}_2+{\bf c}_3)^T {\bf z} +r_0+r_1+r_2\]

これは変分量子固有ソルバーに渡すことができます。

参考文献#

[1] G. Cornuejols, M. L. Fisher, and G. L. Nemhauser, Location of bank accounts to optimize float: an analytical study of exact and approximate algorithms, Management Science, vol. 23(8), 1997

[2] E. Farhi, J. Goldstone, S. Gutmann e-print arXiv 1411.4028, 2014

[3] G. Cornuejols and R. Tutuncu, Optimization methods in finance, 2006

[4] DJ. Berndt and J. Clifford, Using dynamic time warping to find patterns in time series. In KDD workshop 1994 (Vol. 10, No. 16, pp. 359-370).

[5] Max-Cut and Traveling Salesman Problem

実装#

まず、必要なモジュールをインポートします。

[1]:

# Import requisite modules
import math
import datetime

import numpy as np
import matplotlib.pyplot as plt

%matplotlib inline

# Import Qiskit packages
from qiskit.circuit.library import TwoLocal
from qiskit_aer.primitives import Sampler
from qiskit_algorithms import NumPyMinimumEigensolver, QAOA, SamplingVQE
from qiskit_algorithms.optimizers import COBYLA
from qiskit_optimization.algorithms import MinimumEigenOptimizer

# The data providers of stock-market data
from qiskit_finance.data_providers import RandomDataProvider
from qiskit_finance.applications.optimization import PortfolioDiversification

次に、2つの銘柄の価格データをダウンロードし、そのペアワイズ類似度行列(逆数を取ることで (0,1] に正規化された __`動的時間伸縮法 <https://en.wikipedia.org/wiki/Dynamic_time_warping>`__ の距離)を計算します。もし、オフラインになっていたり、一日のアクセス制限を超えていたりして、計算に失敗した場合は、代わりに定数行列を検討します。

[2]:

# Generate a pairwise time-series similarity matrix
seed = 123

stocks = ["TICKER1", "TICKER2"]
n = len(stocks)

data = RandomDataProvider(
    tickers=stocks,
    start=datetime.datetime(2016, 1, 1),
    end=datetime.datetime(2016, 1, 30),
    seed=seed,
)
data.run()
rho = data.get_similarity_matrix()

今度はクラスターの数を決めます。これはロードした株式数よりも小さくする必要があります。

[3]:

q = 1  # q less or equal than n

IBM ILOG CPLEXを使用した古典的なソリューション#

古典的な解法（従来のソリューション）では、IBM CPLEXを使用しています。CPLEXはこの問題の正確な解決策を見つけることができます。 まず、問題をCPLEXが解決できる方法でエンコードし、クラスをインスタンス化して解決するClassicalOptimizerクラスを定義します。

[4]:

class ClassicalOptimizer:
    def __init__(self, rho, n, q):

        self.rho = rho
        self.n = n  # number of inner variables
        self.q = q  # number of required selection

    def compute_allowed_combinations(self):
        f = math.factorial
        return int(f(self.n) / f(self.q) / f(self.n - self.q))

    def cplex_solution(self):

        # refactoring
        rho = self.rho
        n = self.n
        q = self.q

        my_obj = list(rho.reshape(1, n**2)[0]) + [0.0 for x in range(0, n)]
        my_ub = [1 for x in range(0, n**2 + n)]
        my_lb = [0 for x in range(0, n**2 + n)]
        my_ctype = "".join(["I" for x in range(0, n**2 + n)])

        my_rhs = (
            [q]
            + [1 for x in range(0, n)]
            + [0 for x in range(0, n)]
            + [0.1 for x in range(0, n**2)]
        )
        my_sense = (
            "".join(["E" for x in range(0, 1 + n)])
            + "".join(["E" for x in range(0, n)])
            + "".join(["L" for x in range(0, n**2)])
        )

        try:
            my_prob = cplex.Cplex()
            self.populatebyrow(my_prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs)

            my_prob.solve()

        except CplexError as exc:
            print(exc)
            return

        x = my_prob.solution.get_values()
        x = np.array(x)
        cost = my_prob.solution.get_objective_value()

        return x, cost

    def populatebyrow(self, prob, my_obj, my_ub, my_lb, my_ctype, my_sense, my_rhs):

        n = self.n

        prob.objective.set_sense(prob.objective.sense.minimize)
        prob.variables.add(obj=my_obj, lb=my_lb, ub=my_ub, types=my_ctype)

        prob.set_log_stream(None)
        prob.set_error_stream(None)
        prob.set_warning_stream(None)
        prob.set_results_stream(None)

        rows = []
        col = [x for x in range(n**2, n**2 + n)]
        coef = [1 for x in range(0, n)]
        rows.append([col, coef])

        for ii in range(0, n):
            col = [x for x in range(0 + n * ii, n + n * ii)]
            coef = [1 for x in range(0, n)]

            rows.append([col, coef])

        for ii in range(0, n):
            col = [ii * n + ii, n**2 + ii]
            coef = [1, -1]
            rows.append([col, coef])

        for ii in range(0, n):
            for jj in range(0, n):
                col = [ii * n + jj, n**2 + jj]
                coef = [1, -1]

                rows.append([col, coef])

        prob.linear_constraints.add(lin_expr=rows, senses=my_sense, rhs=my_rhs)

[5]:

# Instantiate the classical optimizer class
classical_optimizer = ClassicalOptimizer(rho, n, q)

# Compute the number of feasible solutions:
print("Number of feasible combinations= " + str(classical_optimizer.compute_allowed_combinations()))

# Compute the total number of possible combinations (feasible + unfeasible)
print("Total number of combinations= " + str(2 ** (n * (n + 1))))

Number of feasible combinations= 2
Total number of combinations= 64

[6]:

# Visualize the solution
def visualize_solution(xc, yc, x, C, n, K, title_str):
    plt.figure()
    plt.scatter(xc, yc, s=200)
    for i in range(len(xc)):
        plt.annotate(i, (xc[i] + 0.015, yc[i]), size=16, color="r")

    plt.grid()

    for ii in range(n**2, n**2 + n):

        if x[ii] > 0:
            plt.plot(xc[ii - n**2], yc[ii - n**2], "r*", ms=20)

    for ii in range(0, n**2):

        if x[ii] > 0:
            iy = ii // n
            ix = ii % n
            plt.plot([xc[ix], xc[iy]], [yc[ix], yc[iy]], "C2")

    plt.title(title_str + " cost = " + str(int(C * 100) / 100.0))
    plt.show()

ソリューションは、星印で選択された銘柄が示され、（類似性を介して）緑色のラインで他の銘柄とのリンクを表示します。

Qiskit を使用した量子コンピューティング・ソリューション#

量子的な解法には、Qiskitを使用します。 まず、問題を解決するための量子アプローチをエンコードするクラスQuantumOptimizerを定義し、それをインスタンス化して解決します。 クラス内で次のメソッドを定義します。

  • exact_solution : イジング・ハミルトニアンが \(Z\) 基底に正しく エンコードされていることを確認するために、次元 \(2^N \times 2^N\) の対称行列を考慮して、古典的に固有値分解を計算することができます。今回の問題では \(n=3\)、つまり \(N = 12\) が多くのノートパソコンの限界のようです。

  • sampling_vqe_solution : サンプリング変数量子固有ソルバー (SamplingVQE) を介して問題 \((M)\) を解きます。

  • qaoa_solution : 量子近似最適化アルゴリズム(QAOA)を介して問題 \((M)\) を解きます。

[7]:

from qiskit_algorithms.utils import algorithm_globals


class QuantumOptimizer:
    def __init__(self, rho, n, q):
        self.rho = rho
        self.n = n
        self.q = q
        self.pdf = PortfolioDiversification(similarity_matrix=rho, num_assets=n, num_clusters=q)
        self.qp = self.pdf.to_quadratic_program()

    # Obtains the least eigenvalue of the Hamiltonian classically
    def exact_solution(self):
        exact_mes = NumPyMinimumEigensolver()
        exact_eigensolver = MinimumEigenOptimizer(exact_mes)
        result = exact_eigensolver.solve(self.qp)
        return self.decode_result(result)

    def sampling_vqe_solution(self):
        algorithm_globals.random_seed = 100
        cobyla = COBYLA()
        cobyla.set_options(maxiter=250)
        ry = TwoLocal(n, "ry", "cz", reps=5, entanglement="full")
        svqe_mes = SamplingVQE(sampler=Sampler(), ansatz=ry, optimizer=cobyla)
        svqe = MinimumEigenOptimizer(svqe_mes)
        result = svqe.solve(self.qp)
        return self.decode_result(result)

    def qaoa_solution(self):
        algorithm_globals.random_seed = 1234
        cobyla = COBYLA()
        cobyla.set_options(maxiter=250)
        qaoa_mes = QAOA(sampler=Sampler(), optimizer=cobyla, reps=3)
        qaoa = MinimumEigenOptimizer(qaoa_mes)
        result = qaoa.solve(self.qp)
        return self.decode_result(result)

    def decode_result(self, result, offset=0):
        quantum_solution = 1 - (result.x)
        ground_level = self.qp.objective.evaluate(result.x)
        return quantum_solution, ground_level

ステップ 1#

quantum optimizer classをパラメーターでインスタンス化します: ここでは類似行列が rho; 資産とクラスタの数がそれぞれ n と q です。

[8]:

# Instantiate the quantum optimizer class with parameters:
quantum_optimizer = QuantumOptimizer(rho, n, q)

ステップ２#

問題をバイナリー形式（IH-QP）としてエンコードします。

整合性チェック: quantum optimizer 内のバイナリー定式化が正しいことを確認してください (i.e., 同じ解で同じコストが得られることを確認)。

[9]:

# Check if the binary representation is correct. This requires CPLEX
try:
    import cplex

    # warnings.filterwarnings('ignore')
    quantum_solution, quantum_cost = quantum_optimizer.exact_solution()
    print(quantum_solution, quantum_cost)
    classical_solution, classical_cost = classical_optimizer.cplex_solution()
    print(classical_solution, classical_cost)
    if np.abs(quantum_cost - classical_cost) < 0.01:
        print("Binary formulation is correct")
    else:
        print("Error in the formulation of the Hamiltonian")
except Exception as ex:
    print(ex)

[0. 1. 0. 1. 0. 1.] 1.000779571614484
[1. 0. 1. 0. 1. 0.] 1.000779571614484
Binary formulation is correct

ステップ３#

問題をZ基底のイジング・ハミルトニアンとしてエンコードしてください。

整合性チェック: 定式化が正しいことを確認してください (i.e., 同じ解で同じコストが得られることを確認)。

[10]:

ground_state, ground_level = quantum_optimizer.exact_solution()
print(ground_state)
classical_cost = 1.000779571614484  # obtained from the CPLEX solution

try:
    if np.abs(ground_level - classical_cost) < 0.01:
        print("Ising Hamiltonian in Z basis is correct")
    else:
        print("Error in the Ising Hamiltonian formulation")
except Exception as ex:
    print(ex)

[0. 1. 0. 1. 0. 1.]
Ising Hamiltonian in Z basis is correct

ステップ 4#

SamplingVQE で問題を解決します。 量子ビットの数によっては時間がかかることがあることに注意してください。6量子ビットの場合は、2015 Macbook Proで15分かかります。 12量子ビットの場合12時間以上かかります。より長い実行の場合、ログをとって作業を監視するのが有益かもしれません。それ以外の場合は、ソリューションが表示されるまで待つだけです。

[11]:

svqe_state, svqe_level = quantum_optimizer.sampling_vqe_solution()
print(svqe_state, svqe_level)

try:
    if np.linalg.norm(ground_state - svqe_state) < 0.01:
        print("SamplingVQE produces the same solution as the exact eigensolver.")
    else:
        print(
            "SamplingVQE does not produce the same solution as the exact eigensolver, but that is to be expected."
        )
except Exception as ex:
    print(ex)

[0. 1. 0. 1. 0. 1.] 1.000779571614484
SamplingVQE produces the same solution as the exact eigensolver.

ステップ5#

ソリューションの視覚化

[12]:

xc, yc = data.get_coordinates()

[13]:

visualize_solution(xc, yc, ground_state, ground_level, n, q, "Classical")
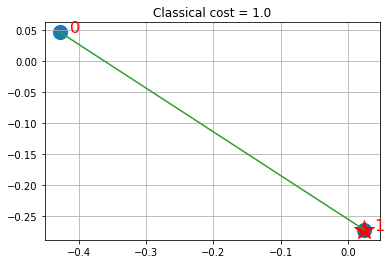
../_images/tutorials_02_portfolio_diversification_24_0.png 
[14]:

visualize_solution(xc, yc, svqe_state, svqe_level, n, q, "SamplingVQE")
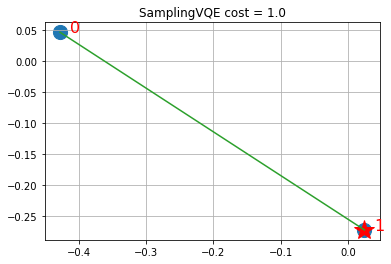
../_images/tutorials_02_portfolio_diversification_25_0.png

ソリューションは、選択された銘柄を星印で示し、緑色の線は、（類似性を介して）ファンド内の他の銘柄との関連性を示しています。ただし、SamplingVQEはイジング・ハミルトニアンのQP定式化におけるヒューリスティックな作用であることに留意してください。Aを適切に選択すると、QP定式化の局所最適解はILP（integer linear program、整数線形計画法）の実行可能解となります。上記のように、いくつかの小さな例では、ILPの最適解と一致するQP定式化の最適解を見つけることができますが、ILPの最適解を見つけることは、一般的には、QP定式化の局所的な最適解を見つけるよりも困難です。SamplingVQEの中でも、特定の変分型（試行波動関数）に対して、より強力な保証を提供することができます。

[15]:

import qiskit.tools.jupyter

%qiskit_version_table
%qiskit_copyright

Version Information

SoftwareVersion
qiskit0.45.0.dev0+ea871e0
qiskit_optimization0.6.0
qiskit_finance0.4.0
qiskit_algorithms0.3.0
qiskit_aer0.12.2
qiskit_ibm_provider0.7.0
System information
Python version3.9.7
Python compilerGCC 7.5.0
Python builddefault, Sep 16 2021 13:09:58
OSLinux
CPUs2
Memory (Gb)5.7784271240234375
Tue Sep 05 15:08:55 2023 EDT

This code is a part of Qiskit

© Copyright IBM 2017, 2023.

This code is licensed under the Apache License, Version 2.0. You may
obtain a copy of this license in the LICENSE.txt file in the root directory
of this source tree or at http://www.apache.org/licenses/LICENSE-2.0.

Any modifications or derivative works of this code must retain this
copyright notice, and modified files need to carry a notice indicating
that they have been altered from the originals.

[ ]: